Построение модели ARMA (p,q)

Построив для наглядности в приложении Statistica 6.0 графики АКФ и ЧАКФ (рисунок 3.1) получили, что АКФ убывает, а ЧАКФ имеет резко выделяющееся значения на 1-м лаге. ЧАКФ подтверждает, что значения АКФ. начиная со второго лага, обусловлены корреляцией на 1-м лаге.

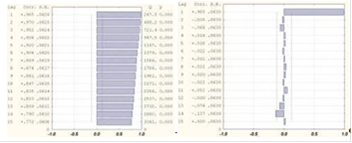
Рисунок 3.1 - АКФ и ЧАКФ для курса AAPL

Согласно свойствам АКФ и ЧАКФ можно предположить [4], что курс акции AAPL описывается моделью ARMA (1,0). Будем строить данную модель в виде:

По выборочным данным в приложении Statistica 6.0 получены оценки коэффициентов модели. Аналитический вид может быть представлен следующим уравнением:

Несмотря на то, что по критерию Стьюдента на 5% -ом уровне значимости свободный член оказался незначим: , но из экономических соображений его не будем удалять из уравнения модели.

По критерию Фишера уравнение регрессии значимо, поскольку

.

Коэффициент детерминации , что говорит об очень хорошем качестве построенной модели. На 98.7% модель ARMA (1,0) аппроксимирует исходные данные временного ряда, остальное приходится на ошибку.

На рисунке 3.2 приведем график остатков модели (3.2).

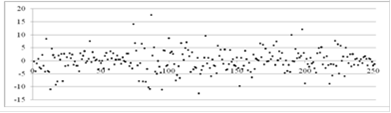
Рисунок 3.2 - График остатков модели (3.2)

Визуальный анализ дает возможность предположить, что ряд остатков является стационарным, поскольку в нем отсутствует определенная направленность. Проверим, выполняются ли для остатков условия Гаусса-Маркова.

. С учетом погрешности в вычислениях математическое ожидание остатков имеет значение .

. Стандартная ошибка регрессии . Несколько значений остатков лежат вне интервала и являются своего рода выбросами, резко выделяющимися на фоне общей картины остатков, что, возможно, вызвано неточностью в вычислениях. Поэтому отклонить или принять гипотезу о нормальном распределении остатков затруднительно. Применяя статистику Жака-Бера, предварительно вычислив коэффициенты асимметрии и эксцесса, установили, что гипотеза о нормальном распределении остатков отклоняется, поскольку значение статистики , что гораздо больше квантили распределения равной 5.991.

. Для проверки остатков на случайность используем критерий "поворотных точек". Для данного ряда остатков получили . Следовательно, выборка остатков случайна.

. Для рассматриваемого ряда остатков при проверке на наличие гетероскедастичности ранговый коэффициент корреляции Спирмена оказался равным . Оценив статистическую значимость с помощью t-критерия: , и сравнив эту величину с табличной при уровне значимости , получили, что . Следовательно, гипотеза об отсутствии гетероскедастичности остатков не отклоняется.

Еще статьи по экономике

Моделирование курса акций AAPL и IBM
В каждой сфере экономики встречаются явления и процессы, которые интересно и важно изучать в их развитии (например, цены, курсы валют, режим протекания производственного процес ...

Характеристика предприятия ООО Электротех
трейдер российский программный комплекс Одним из наиболее важных этапов подготовки специалистов инженерных специальностей является прохождение ими практики в сторонних организац ...

Товарооборачиваемость анализ и пути ускорения с целью увеличения прибыли и рентабельности Гродненского облпотребсоюза
Изучение товарных запасов и товарооборачиваемости относится к числу важных задач экономики торговли. Значение статистического учета и анализа товарных запасов определяется их р ...