Модель ARIMA (p,d,q)

Основными инструментами идентификации порядка модели ARIMA (p,d,q) являются графики АКФ и ЧАКФ [3]. Также при построении модели в первую очередь необходимо проверить рассматриваемый ряд на стационарность. Признаками не стационарности являются наличие тренда, гетероскедастичность, изменяющаяся автокорреляция.

Проанализируем АКФ и ЧАКФ рассматриваемого ряда. Их графические представления уже были приведены па рисунке 3.1 График АКФ позволяет предположить, что исходный временной ряд может быть описан авторегрессионным процессом с коэффициентом при лаговой переменной, близким к 1, т.е. это говорит о не стационарности процесса, поскольку АКФ убывает очень медленно [12].

Подтверждением служит проверка ряда с помощью статистики Дики-Фуллера (1.22), которая при уровне значимости выдает значение t-статистики , что говорит о не стационарности ряда.

Одним из способов приведения ряда к стационарному виду является дифференцирование ряда [3]. Рассмотрим ряд, полученный из исходного ряда взятием разности 1-го порядка. Глядя на рисунок 3.4 можно заметить, что полученный с помощью дифференцирования ряд уже больше похож на стационарный - в нем отсутствует тренд.

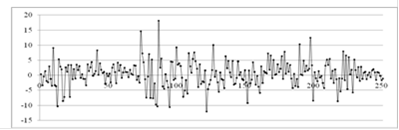
Рисунок 3.4 - Продифференцированный ряд значений цены акции AAPL

Проверку ряда на стационарность проведем теперь с помощью интеграционной статистики Дарбина-Уотсона. Применняя формулу (1.21) для уровней исходного ряда цен находим значение статистики

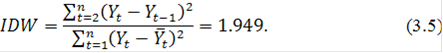
Рассчитанное значения статистики (3.5) очень близко к 2, что позволяет принять гипотезу о стационарности ряда. Таким образом, исходный ряд приведен к стационарному виду взятием разности первого порядка, следовательно, .

Внешний вид АКФ и ЧАКФ (рисунок 3.5) дают основание предположить, что полученный дифференцированием ряд является "белым шумом". Q-статистика Люинга-Бокса подтверждает выдвинутое предположение, т.к. рассчитанные значения не превосходят критических (табличных) значений статистики на 5% -ом уровне значимости. Следовательно, процесс является "белым шумом".

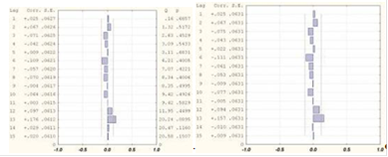
Рисунок 3.5 - АКФ и ЧАКФ продифференцированного ряда курса AAPL

Исходя из полученных результатов анализа, приходим к выводу, что рассматриваемый ряд можно описать моделью ARIMA (p,1,q).

По внешнему виду графиков не всегда удается определить оптимальные параметры модели [1], что характерно для нашей ситуации. Поэтому построим модели ARIMA (1,1,0), ARIMA (0,1,1), ARIMA (2,1,2), ARIMA (3,1,2), ARIMA (6,1,3) и сравним их по информационным критериям Акаики и Шварца (1.23,1.24).

Построение моделей производим в программе Statistica 6.0, в результате после исключения незначимых коэффициентов получены следующие уравнения:

Еще статьи по экономике

Иностранные инвестиции
Актуальность исследуемого вопроса, следует из того, что современная мировая экономика не может успешно развиваться без иностранных инвестиций. Многие страны мира активно инвестируют свои сре ...

Исследование в экономике теории магистралей
В экономической теории на первоначальном этапе ее развития редко использовались математические формулировки. Тем не менее, многие классические доктрины экономики в словесной, ...

Исследование хозяйства ЗАО Куликовское на основе экономико-статистического анализа себестоимости
В данной курсовой работе изучено хозяйство ЗАО "Куликовское" Калачиснкого района. Изучение данного хозяйства происходит на основе анализа себестоимости зерна. Зерновые являютс ...