Методы вычисления теорий магистралей

На основе модели Неймана могут быть построены различные оптимизационные задачи. Одна из возможных постановок выглядит так:

(17)

при ограничениях

(18)

В этой задаче требуется найти такую траекторию , чтобы доход от продажи всего выпуска к концу планового периода был максимальным при условии, что затраты каждого периода не превышают выпусков предыдущего периода.

Всякую траекторию, удовлетворяющую условиям и доставляющую максимальное значение целевой функции, будем называть оптимальной траекторией и обозначать через (здесь - установившаяся к началу планового периода интенсивность выпуска). В общем случае в данной задаче может существовать не одна оптимальная траектория (Приложение А, А-2).

Предположим, что в модели Неймана существует единственная стационарная траектория производства, соответствующая максимальному темпу сбалансированного роста , т.е.

Поскольку , где в любой момент t есть скаляр, то вместо предыдущего неравенства можно писать . Далее, имея в виду представление , мы условно можем написать .

В дальнейшем нам понадобится понятие "расстояния" между векторами интенсивностей в пространстве . Под расстоянием между двумя векторами интенсивностей , будем понимать число

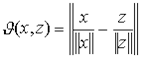(19)

где - норма вектора, т.е. число, равное длине данного вектора. Объясним наглядно смысл такого расстояния. Для удобства обозначим . Тогда

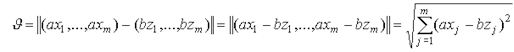(20)

Далее, для любого вектора x длина вектора равна единице. Действительно, так как норма числа есть само число, то

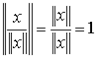
Например, для имеем:

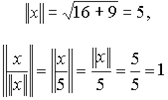(Приложение Б, рисунок Б-4)

Поэтому равно длине отрезка между точками , , лежащими на единичной окружности. Из этого рисунка видно: 1) если возможно представление , где (т.е. x и z коллинеарные вектора), то ;

) для , .

Нетрудно видеть, что есть непрерывная по обоим аргументам функция.

С помощью введенного понятия расстояния дадим строгое определение понятия магистрали.

Определение. Луч Неймана называется сильной магистралью в задаче (1-2), если для каждого существуют такие зависящие от (но не зависящие от T) числа и , что для всякой оптимальной траектории этой задачи и для всех (Приложение А, А-3).

Еще статьи по экономике

Характеристика машиностроения, металлообработки, приборостроения Удмуртии
Машиностроение, металлообработка и приборостроение - исторически сложившаяся специализация промышленности Удмуртии. По настоящее время машиностроение, металлообработка и прибор ...

Коммерческая деятельность совместных предприятий
Актуальность темы исследования. В современном мире экономика любого государства не может успешно и динамично развиваться без интеграции в мировое хозяйство, без участия в проц ...

Классические социально-экономические истоки теории организации
Современный мир нередко рассматривается как мир организаций, которые представляют собой совокупность людей и групп, объединенных для достижения какой-либо цели, решения той ил ...