Методы вычисления теорий магистралей
Неразложимая матрица A называется устойчивой, если для любого x последовательность ![]() сходится, где
сходится, где ![]() - k-ая степень матрицы
- k-ая степень матрицы![]() ,
, ![]() - число Фробениуса для матрицы A. Предельной точкой этой последовательности при
- число Фробениуса для матрицы A. Предельной точкой этой последовательности при ![]() и
и ![]() является вектор
является вектор 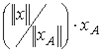 , где
, где ![]() - вектор Фробениуса для матрицы A (Приложение А, А-8).
- вектор Фробениуса для матрицы A (Приложение А, А-8).
Примитивная матрица всегда устойчива.
Относительно задачи (3-4) сделаем следующие предположения:
1. ![]() ;
;
2. матрица A неотрицательна, неразложима и примитивна.
Теорема. Если выполнены условия 1), 2), то сильной магистралью в задаче (21-22) является вектор Фробениуса ![]() матрицы A, т.е.
матрицы A, т.е. ![]() , где
, где ![]() - стационарная траектория динамической модели Леонтьева (4) (
- стационарная траектория динамической модели Леонтьева (4) (![]() ).
).
Целевая функция в задаче (21-22) относится к конечному моменту планового периода и называется терминальной. В динамической оптимизационной задаче Леонтьева с нетерминальной целевой функцией возникает так называемая проблема горизонта планирования. Дело в том, что по оптимальной траектории выпуск к моменту T может оказаться недостаточным для обеспечения нормального функционирования экономики за горизонтом планирования. Поэтому требуется наложить специальные ограничения снизу на вектор ![]() , что приводит к дополнительным сложностям при исследовании магистральных свойств оптимальных траекторий.
, что приводит к дополнительным сложностям при исследовании магистральных свойств оптимальных траекторий.
Вернемся теперь к задаче Неймана (17-18) и предположим выполненными следующие условия:
а) существует такое число ![]() , что соотношения
, что соотношения ![]() определяют единственный вектор
определяют единственный вектор ![]() ; б)
; б) ![]() в) существует стационарная траектория цен
в) существует стационарная траектория цен ![]() ; г) матрица A неотрицательна, неразложима и примитивна; д) для любого достаточно малого числа
; г) матрица A неотрицательна, неразложима и примитивна; д) для любого достаточно малого числа ![]() существуют такие (зависящие от
существуют такие (зависящие от ![]() ) числа
) числа ![]() и
и ![]() , что для оптимальной траектории
, что для оптимальной траектории ![]() из неравенства
из неравенства ![]() вытекают неравенства
вытекают неравенства ![]()
В последнем условии A1 и B1 - это такие подматрицы матриц A и B
(![]() ), что
), что ![]() .
.
В отличие от условий а-г, допускающих соответствующие экономические интерпретации, условие е) носит чисто технический характер и нужно сугубо для доказательства следующей теоремы.
Теорема. При выполнении условий а-д для любого ![]() существует такое число
существует такое число ![]() , не зависящее от T, что для любой оптимальной траектории
, не зависящее от T, что для любой оптимальной траектории ![]() задачи (17-18) выполняется условие
задачи (17-18) выполняется условие ![]() для всех
для всех ![]()
Еще статьи по экономике
Комплексный экономический анализ хозяйственной деятельности предприятия ОАО РЖД
Любое предприятие сталкивается с необходимость проведения анализа своей
финансово-хозяйственной деятельности. Результаты такого анализа позволяют
оценить текущее финансовое сос ...
Металлургия цветных металлов
Общая характеристика отрасли
Металлургический комплекс - это взаимообусловленное сочетание
следующих технологических процессов:
· добыча и подготовка сырья к перер ...
Механизмы и способы управления доходами предприятия
В
рыночной экономике действует такая форма организации хозяйственной
деятельности, в которой потребители и производители действуют самостоятельно,
на основании экономических м ...
