Моделирование тенденции временного ряда акции IBM при наличии структурных изменений

Рассматривается временной ряд, составленный из 252 значений цены акции IBM (приложение А), взятых за год, за период с 4 января 2010 г. по 31 декабря 2010 г. Значения являются ежедневными, в неделе 5 дней торгов.

В первую очередь приведем график исходных данных (зависимость цены акции от даты торгов), он имеет вид:

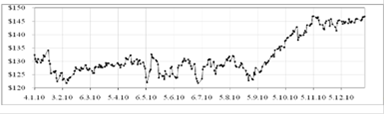
Рисунок 2.6 - График исходных данных для курса акции IBM

Рассматриваемый ряд данных характеризуется нестабильной тенденцией. Ряд содержит значительное количество мелких скачков. Динамика представляет собой три периода развития. В начальный период цена интенсивно колеблется и имеет среднее значение около 127$, во втором периоде на протяжении двух месяцев с 6 сентября по 5 ноября цена стремительно растет, несмотря на один резкий скачок 18 октября. Цена становится достаточно стабильной без резких "перепадов" (около 146$) только в третий период, приходящийся на последний месяц.

Резкие "перепады", как правило, происходят в результате воздействия на исследуемый ряд внешних факторов, в том числе изменения в политике компании. Всплески зависят от экономических и политических стратегий на финансовом рынке. К примеру, неожиданный всплеск произошел с 6 сентября по 5 ноября 2010 года.

После публикации финансовых результатов корпорации IBM стало известно, что получить подобный результат удалось за счет того, что бизнес-клиенты IBM по всему миру активно стали внедрять у себя дорогое серверное оборудование в целом и дорогие мейнфреймы семейства System Z в частности.

Метод Форстера-Стюарта, примененный к ряду курса акции IBM, выявил наличие тренда, поскольку вычисленные по формуле (1.7) статистики и . Поэтому подберем тренд и построим модель, не принимая для начала во внимания структурное изменение.

Подбор трендовой модели

При подборе линий тренда к графику исходных данных было выявлено (рисунок 2.7), что лишь полиномиальный тренд пятой степени наиболее точно соответствуют тенденции исследуемого ряда.

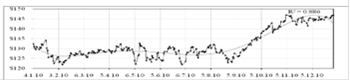
Рисунок 2.7 - График общей полиномиальной модели для курса IBM

Модель имеет следующий вид:

Коэффициенты детерминации . Значит, построенная полиномиальная модель (2.14) аппроксимирует исходные данные на 88.6%, остальные 11.4% приходятся на ошибки. Т.е. полиномиальный тренд 5-го порядка достаточно хорошо описывает ряд. При рассмотрении полиномов более высокого порядка можно заметить, что с увеличением степени полинома, величина коэффициента детерминации практически не меняется: для полиномиальной модели 6-й степеней коэффициент детерминации равен 0.887. Таким образом, будем рассматривать полиномиальную модель 5-го порядка.

Используем критерий Стьюдента и критерий Фишера с уровнем значимости 0.05 для проверки значимости коэффициентов и уравнения полиномиальной регрессии в целом.

Еще статьи по экономике

Характеристика машиностроения, металлообработки, приборостроения Удмуртии
Машиностроение, металлообработка и приборостроение - исторически сложившаяся специализация промышленности Удмуртии. По настоящее время машиностроение, металлообработка и прибор ...

Использование механизма государственно-частного партнерства
В настоящее время в рамках неустойчивой экономической ситуации в России и мире усиливается тенденция к активизации отношений государства и частного бизнеса в направлении решени ...

Источники формирования основных и оборотных средств на предприятии ЗАО Василиса
Материально-технической основой производства на любом предприятии являются производственные фонды, представляющие собой функционирующие в процессе деятельности предприятия сре ...